Ulike måter å bevise Pythagoras teoremåte: eksempler, beskrivelse og omtaler

I ett kan du være sikker på ett hundre prosentprosent, at spørsmålet om hva som er lik plassen av hypotenusen, vil enhver voksen person med modig svar svare: "Summen av kvadratene på bena." Denne teorien er fast forankret i alle utdannede personers sinn, men du må bare be noen om å bevise det, og da kan det være vanskeligheter. Derfor, la oss huske og vurdere ulike måter å bevise den pythagorasiske setningen på.

Oversikt over biografi

Pythagorasetningen er kjent for nesten alle, menAv en eller annen grunn er biografien til personen som produserte den, ikke så populær. Det kan repareres. Derfor, før du studerer de ulike metodene for å bevise Pythagorasetningen, er det nødvendig å kortlegge seg kjent med hans personlighet.

Pythagoras er en filosof, matematiker, tenker fraAntikkens Hellas. I dag er det veldig vanskelig å skille sin biografi fra legender som har dannet til minne om denne store mannen. Men som følge av hans etterfølgere ble Pythagoras of Samos født på øya Samos. Hans far var en vanlig steinkutter, men moren hans kom fra en edel familie.

Ifølge legenden, fødselen av Pythagorasspådde en kvinne kalt Pythia, i sin ære og kalt gutten. Ifølge hennes prediksjon skulle en født gutt bringe mye nytte og godt til menneskeheten. Hva gjorde han egentlig.

Fødsel av stolen

I sin ungdom flyttet Pythagoras fra Samos tilEgypt å møte kjente egyptiske vismenn der. Etter å ha møtt dem, fikk han lov til å lære hvor han lærte alle de store prestasjonene i egyptisk filosofi, matematikk og medisin.

Sannsynligvis var det i Egypt at Pythagoras ble inspirertmajestet og skjønnhet i pyramidene og skapt sin store teori. Dette kan sjokkere lesere, men moderne historikere tror at Pythagoras ikke viste sin teori. Men han passerte kun sin kunnskap til sine etterfølgere, som senere fullførte alle nødvendige matematiske beregninger.

Uansett, i dag er det ikke kjent.metode for bevis på denne setningen, men flere samtidig. I dag gjenstår det bare å gjette hvordan de gamle grekerne har gjort sine beregninger, så her vurderer vi ulike måter å bevise den pythagoranske satsen.

Pythagorasetning

Før du starter noen beregninger, må du finne ut hvilken teori du skal bevise. Pythagorasetningen høres ut som dette: "I en trekant hvor en av vinklene er 90^omtrent, summen av rutene på bena er lik plassen av hypotenusen. "

Det er 15 forskjellige måter å bevise pythagorasetningen. Dette er ganske stort antall, så vi vil være oppmerksomme på de mest populære.

Metode en

Først angir vi hva som er gitt til oss. Disse dataene vil bli utvidet til andre metoder for bevis på pythagorasetningen, så du bør umiddelbart huske alle eksisterende betegnelser.

Anta at en rettvinklet trekant er gitt, med a og b katetre lik c. Den første bevismetoden er basert på behovet for å tegne et firkant fra en riktig trekant.

For å gjøre dette trenger du benlengden aå tegne et segment som er lik benet og omvendt. Så det burde være to like sider av torget. Det gjenstår bare å tegne to parallelle linjer, og kvadratet er klart.

Inne i den resulterende figuren må du tegne meren firkant med en side som er lik hypotenusen til den opprinnelige trekanten. For å gjøre dette, må du tegne to parallelle segmenter som er lik c, fra kryssene til ac og sv. Dermed er det tre sider av torget, hvorav en er hypotenusen til de originale høyre trekanter. Det gjenstår bare å tegne det fjerde segmentet.

Basert på det resulterende mønsteret kan vi konkludere med at arealet på det ytre torget er (a + b)². Hvis du ser inne i figuren, kan du se at i tillegg til det indre torget er det fire rettvinklede trekanter. Arealet av hver er 0,5.

Derfor er området: 4 * 0.5av + s²= 2av + s²

Herfra (a + c)²= 2av + s²

Og derfor med²= a²+ inn²

Stillingen er bevist.

Metode to: lignende trekanter

Denne formelen er bevis på pythagorasetningenble avledet på grunnlag av en uttalelse fra delen av geometri om lignende trekanter. Det står at benet til en riktig trekant er gjennomsnittlig proporsjonal med sin hypotenuse og segmentet av hypotenuse som kommer fra toppen av 90^omtrent.

De opprinnelige dataene forblir de samme, så vi starter umiddelbart med beviset. Utfør vinkelrett på sidens AB-segment SD. Basert på ovennevnte uttalelse er trekantens bein like:

AC = √AB * AD, CB = √ AB * DV.

For å svare på spørsmålet om hvordan å bevise Pythagorasetningen, må beviset legges ut ved å kvadratere begge ulikheter.

AS²= AB * HELL og SV²= AB * DV

Nå må vi legge til den resulterende ulikheten.

AS²+ SV²= AB * (HELL * LW), hvor HELL + LW = AV

Det viser seg at:

AS²+ SV²= AB * AB

Og derfor:

AS²+ SV²= AB²

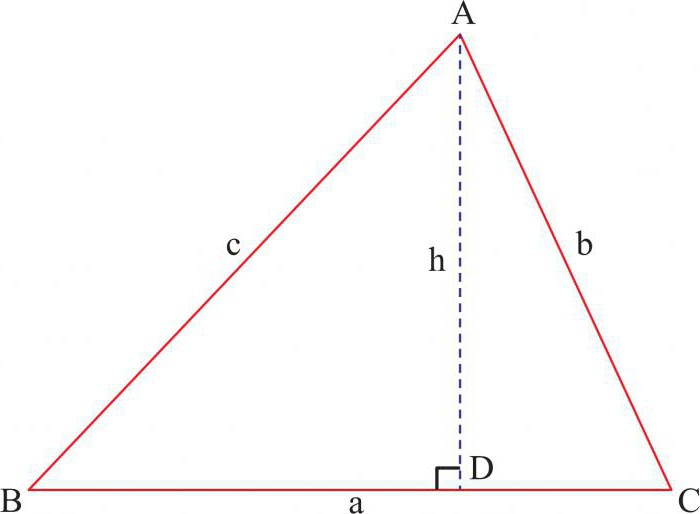
Beviset om pythagorasetningen og de ulike måtene å løse det trenger en mangesidig tilnærming til dette problemet. Dette alternativet er imidlertid en av de enkleste.

En annen beregningsmetode

Beskrivelse av ulike måter å bevise teoremet påPythagoras kan ikke si noe om noe før du begynner å trene deg selv. Mange metoder involverer ikke bare matematiske beregninger, men også bygging av nye figurer fra den opprinnelige trekant.

I dette tilfellet er det nødvendig å fullføre en mer rettvinklet trekant av AF. Således er det nå to trekanter med en felles BC.

Å vite at områdene av slike figurer har et forhold som kvadrater av deres tilsvarende lineære dimensjoner, da:

S_ABC * med²- S_AVD* i² = S_AVD* a²- S_IRR* a²

S_ABC* (med²-i²) = a²* (S_AVD-S_IRR)

med²-i²= a²

med²= a²+ inn²

Siden fra ulike metoder for å bevise Pythagorasetningen for 8. klasse er dette alternativet lite egnet, kan du bruke følgende metode.

Den enkleste måten å bevise pythagorasetningen. anmeldelser

Historikere tror at dette var første gangpleide å bevise teorien i antikkens Hellas. Det er det enkleste, siden det krever absolutt ingen beregninger. Hvis du tegner bildet riktig, så er beviset på setningen som²+ inn²= med² vil være tydelig synlig.

Betingelsene for denne metoden vil avvike noe fra den forrige. For å bevise teorien, anta at den riktige trekant ABC er ensidig.

Vi tar hypotenusu AS for siden av torget ogVi er tre av sine fester. I tillegg må du tegne to diagonale linjer i den resulterende firkanten. Så inne i det er det fire isosceles trekanter.

Til AV- og SV-kattene er det også nødvendig å tegne en firkant og tegne en diagonal rett linje i hver av dem. Den første rette linjen trekkes fra toppunktet A, den andre - fra C.

Nå må du nøye se på det resulterende bildet. Siden det er fire trekanter på AC-hypotenusen, lik originalet og to på bena, indikerer dette sannheten i denne setningen.

Forresten, takket være denne metoden for å bevise pythagorasetningen, ble den berømte frasen født: "Pythagoranske bukser er like i alle retninger."

Bevis for J. Garfield

James Garfield er den tyvende presidenten i USA. Foruten det faktum at han forlot sitt merke i historien som hersker i USA, var han også begavet med selvlært.

I begynnelsen av karrieren var han vanligen lærer i folkeskole, men ble snart direktør for en av de høyere utdanningsinstitusjonene. Strivet for selvutvikling og tillot ham å foreslå en ny teori om bevis på pythagorasetningen. Stillingen og et eksempel på løsningen er som følger.

Først må du trekke på et stykke papir torettvinklede trekanter slik at benet til en av dem er en fortsettelse av den andre. Knektene til disse trekanter må kobles for å ende opp med en trapesform.

Som kjent er området av en trapesform lik produktet av halv summen av dets baser og dets høyde.

S = a + b / 2 * (a + b)

Hvis vi ser på den resulterende trapesformen som en figur bestående av tre trekanter, så kan området bli funnet på følgende måte:

S = AV / 2 * 2 + s²/ 2

Nå må du balansere de to kildeuttrykkene

2av / 2 + s / 2 = (a + b)²/ 2

med²= a²+ inn²

Om Pythagorasetningen og hvordan du kan bevise det, kan du skrive mer enn ett volum i læreboken. Men er det fornuftig når denne kunnskapen ikke kan gjøres i praksis?

Praktisk anvendelse av Pythagorasetningen

Dessverre, i moderne skoleprogrammerDenne teormen kan bare brukes i geometriske problemer. Nyutdannede vil snart forlate skolens vegger, uten å vite hvordan de skal bruke sin kunnskap og ferdigheter i praksis.

Faktisk, bruk Pythagorasetningen ialle kan ta vare på sitt daglige liv. Og ikke bare i profesjonelle aktiviteter, men også i vanlige husholdningsarbeid. La oss se på flere tilfeller der Pythagorasetningen og metodene for beviset kan være ekstremt nødvendige.

Kommunikasjonsteori og astronomi

Det ser ut som at stjerner og trekanter kan kobles på papir. Faktisk er astronomi et vitenskapelig felt der den pythagoriske teorem er mye brukt.

For eksempel vurdere bevegelsen av en lysstråle i rommet. Det er kjent at lyset beveger seg i begge retninger med samme hastighet. Banen til AB, som beveger lysstrålen, kalles l. Og halvparten av tiden det tar for lyset å komme fra punkt A til punkt B kalles t. Og strålehastigheten - c. Det viser seg at: c * t = l

Hvis du ser på denne strålen av en annenet fly, for eksempel fra en romfartøy, som beveger seg med en hastighet v, så med en slik observasjon av kroppene vil deres fart endre seg. I dette tilfellet vil selv stasjonære elementer bevege seg med hastigheten v i motsatt retning.

Anta at en komisk liner flyter til høyre. Da flyttes punktene A og B, mellom hvilke strålen kastes, til venstre. Videre, når strålen beveger seg fra punkt A til punkt B, har punkt A tid til å bevege seg, og følgelig kommer lyset til et nytt punkt C. ").

d = t "* v

Og for å finne avstanden som en lysstråle kunne passere i løpet av denne tiden, må du betegne en halv av banen til en ny bøk s og få følgende uttrykk:

s = c * t "

Hvis du forestiller deg at lyspunktene er C og B, ogSiden mellomrommet er toppunktet av en likestillet trekant, deler segmentet fra punkt A til liner det i to høyre trekanter. Derfor, takket være Pythagorasetningen, kan du finne avstanden som en lysstråle kunne passere.

s² = l² + d²

Dette eksemplet er selvfølgelig ikke det mest vellykkede, siden bare noen få kan være heldige nok til å prøve det i praksis. Derfor vurderer vi mer verdslige varianter av anvendelsen av denne setningen.

Mobil Signal Radius

Moderne liv kan ikke lenger forestilles uten at det finnes smarttelefoner. Men hvor mye ville være fra dem, hvis de ikke kunne koble abonnenter via mobilkommunikasjon?

Kvaliteten til mobilkommunikasjon avhenger direkte avhøyden på mobiloperatørens antenne. For å beregne hvor langt fra mobiltårnet kan telefonen motta et signal, kan du bruke Pythagorasetningen.

Anta at du må finne omtrentlig høyde på et fast tårn, slik at det kan formere et signal innenfor en radius på 200 kilometer.

AB (tårnhøyde) = x;

SU (radius av signaloverføring) = 200 km;

OS (radius av kloden) = 6380 km;

Herfra

OB = OA + ABOV = r + x

Ved bruk av Pythagorasetningen finner vi ut at minimumshøyden på tårnet skal være 2,3 kilometer.

Pythagorasetningen i hverdagen

Merkelig nok, kan den pythagoranske teorem vise seg å værenyttig selv i hjemlige forhold, for eksempel å bestemme høyden på skapet, for eksempel. Ved første øyekast er det ikke nødvendig å bruke slike komplekse beregninger, fordi du bare kan ta målinger ved hjelp av roulette. Men mange lurer på hvorfor det er visse problemer i monteringsprosessen hvis alle målinger er tatt mer enn nøyaktig.

Faktum er at garderoben kommer tilhorisontal posisjon og bare da stiger og installeres mot veggen. Derfor skal kabinetsiden i løfteprosessen være fri til å passere både i høyde og diagonalt i rommet.

Anta at det er en garderobe med en dybde på 800 mm. Avstanden fra gulv til tak er 2600 mm. En erfaren furniture maker vil si at høyden på kabinettet skal være 126 mm mindre enn romets høyde. Men hvorfor akkurat 126 mm? Tenk på et eksempel.

Med ideelle kabinettdimensjoner, kontrollerer vi effekten av Pythagorasetningen:

AC = √AB²+ √ВС²

AC = √2474²800²= 2600 mm - alt passer.

Anta at kabinets høyde ikke er lik 2474 mm, men 2505 mm. deretter:

AC = √2505²+ √800²= 2629 mm.

Derfor er dette skapet ikke egnet for installasjon i dette rommet. Siden når den heves i vertikal stilling, kan kroppen bli skadet.

Kanskje, etter å ha vurdert ulike måter å bevisePythagorasetninger av forskjellige forskere, kan vi konkludere med at det er mer enn sant. Nå kan du bruke informasjonen mottatt i ditt daglige liv og være helt sikker på at alle beregninger ikke bare er nyttige, men også sanne.