Maclaurin-serien og dekomponeringen av visse funksjoner

Å studere høyere matematikk bør være kjent,at summen av en maktserie som tilhører konvergensintervallet i den angitte serien, er en differensieringsfunksjon som er kontinuerlig og uendelig mange ganger forskjellig. Spørsmålet oppstår: Er det mulig å hevde at en gitt vilkårlig funksjon f (x) er summen av en kraftserie? Det er under hvilke forhold kan f-f f (x) representeres av en kraftserie? Betydningen av et slikt spørsmål er at det er mulig å omtrent erstatte f (x) med summen av flere første termer av kraftserien, det vil si et polynom. En slik substitusjon av en funksjon ved et ganske enkelt uttrykk, et polynom, er også praktisk ved å løse visse problemer med matematisk analyse, nemlig: ved å løse integraler, beregne differensialligninger og så videre.

Det er bevist at for noen f-funksjon f (x) der det er mulig å beregne derivatene opp til (n + 1) -t rekkefølge, inkludert den siste, i nærheten av (a - R; x₀ + R) av noe punkt x = a, er følgende formel gyldig:

Denne formelen bærer navnet på den berømte forskeren Brooke Taylor. Serien som er hentet fra den forrige, kalles Maclaurin-serien:

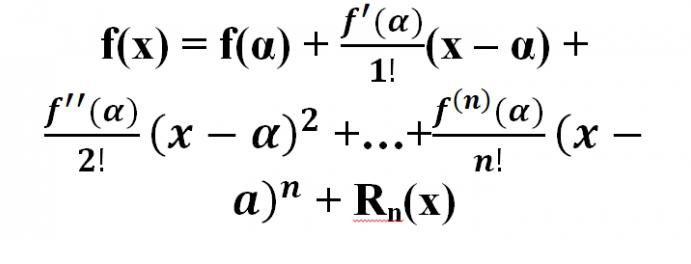
En regel som gjør det mulig å dekomponere til en Maclaurin-serie:

1. Bestem derivatene av den første, andre, tredje ... bestillingen.
2. Beregn hva derivatene ved x = 0 er lik.
3. Ta opp Maclaurin-serien for en gitt funksjon, og bestemm deretter intervallet for konvergensen.
4. Bestem intervallet (-R; R), der resten av Maclaurin-formelen

R_n(x) -> 0 som n -> uendelig. I tilfelle der det eksisterer, må funksjonen f (x) i den sammenfalle med summen av Maclaurin-serien.

Vi vurderer nå Maclaurin-serien for individuelle funksjoner.

1. Dermed er den første f (x) = e^x. Selvfølgelig har en slik funksjon med hensyn til dens egenskaper derivater av de mest varierte ordrene, med f^(K)(x) = e^xhvor k er lik alle naturlige tall. Erstatter x = 0. Få f^(K)(0) = e⁰= 1, k = 1,2 ... Basert på ovenstående, raden e^x ville se slik ut:

2. Maclaurin-serien for funksjonen f (x) = sin x. Forklar umiddelbart at f-Ia for alle ukjente vil ha derivater, foruten f^"(x) = cos x = sin (x + n / 2), f^""(x) = -in x = sin (x + 2 * n / 2) ..., f^(K)(x) = sin (x + k * n / 2), hvor k er lik alle naturlige tall. Det er, etter å ha gjort enkle beregninger, kan vi komme til den konklusjon at serien for f (x) = sin x vil ha følgende form:

3. Nå skal vi prøve å vurdere f-yy f (x) = cos x. Det for alle ukjente har derivater av vilkårlig rekkefølge, og | f^(K)(x) | = | Cos (x + k * n / 2) | <= 1, k = 1,2 ... Igjen, det å ha gjort noen beregninger, finner vi at serien for f (x) = cos x vil se slik ut:

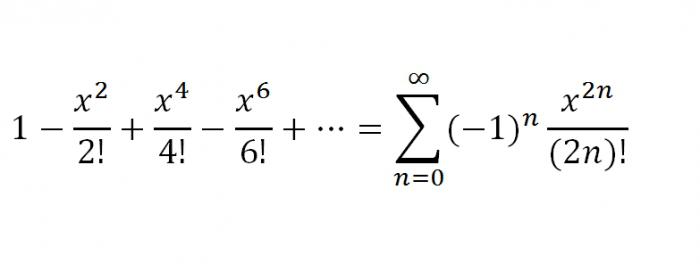
Så, vi har oppført de viktigste funksjonene somkan dekomponeres i en Maclaurin-serie, men de suppleres av Taylor-serien for noen funksjoner. Nå vil vi liste dem. Det er også verdt å merke seg at Taylor og Maclaurin-serien er en viktig del av verkstedet for å løse serier i høyere matematikk. Så, Taylor rangerer.

1. Den første blir en serie for funksjonen f (x) = ln (1 + x). Som i de foregående eksemplene kan vi for gitt f (x) = ln (1 + x) legge til en serie ved hjelp av den generelle formen for Maclaurin-serien. For denne funksjonen kan Maclaurin-serien imidlertid oppnås mye lettere. Integrerer en bestemt geometrisk serie, vi får en serie for f (x) = ln (1 + x) av en slik prøve:

2. Og den andre, som vil være endelig i vår artikkel, vil være en serie for f (x) = arctan x. For x som tilhører intervallet [-1; 1], er dekomponeringen gyldig:

Det er alt. Denne artikkelen undersøkte den mest brukte Taylor og Maclaurin-serien i høyere matematikk, spesielt i økonomiske og tekniske universiteter.